Um problema de xadrez popular conhecido como “problema das oito rainhas” tem cativado matemáticos e cientistas da computação há anos, mas ninguém foi capaz de criar um programa de computador que conseguisse resolver o enigma de forma rápida e eficiente. Pesquisadores do Reino Unido afirmam agora que os computadores nunca estarão à altura da tarefa e estão oferecendo US$ 1 milhão para quem conseguir provar que eles estão errados.
O problema das oito rainhas existe desde a década de 1850 e desafia o jogador a colocar oito rainhas em um tabuleiro de xadrez convencional sem outras peças de tal forma que nenhuma rainha ameace qualquer outra. Isso é muito difícil, dado o imenso poder da Rainha; o jogador deve garantir que cada rainha seja colocada em sua própria coluna, mas de tal forma que nenhuma rainha ameace outra ao longo de outras linhas e diagonais.
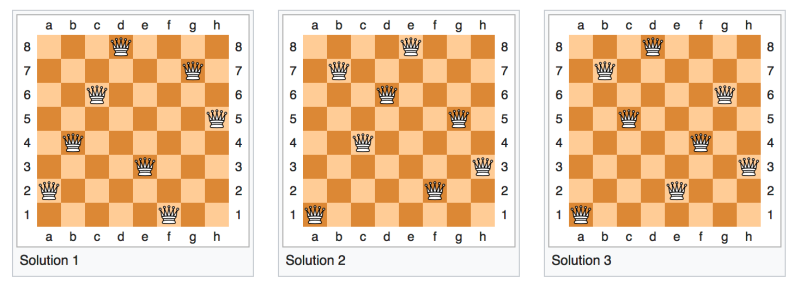
Três das 92 soluções para o problema das oito rainhas. As soluções parecem simples, mas chegar até elas é um tremendo desafio computacional. (Imagem: Wikimedia)
Esse enigma foi resolvido por seres humanos (há 92 soluções fora dos 4.426.165.368 possíveis arranjos de oito rainhas em um tabuleiro 8 x 8), mas continua a representar um desafio fascinante e complexo para os matemáticos e cientistas da computação, particularmente quando o tabuleiro é dimensionado para além do padrão de oito por oito. Quando o tabuleiro se torna maior e mais rainhas são acrescentadas, cria-se um problema que, como um novo artigo publicado no The Journal of Artificial Intelligence Research aponta, é quase impossível para um computador resolver em uma quantidade razoável de tempo.
Os programas de computador tendem a ter uma abordagem de “força bruta” para o problema, sistematicamente passando por todas as permutações possíveis. É por isso que o problema das oito rainhas é considerado “computacionalmente caro”, em que o número total de combinações pode chegar a quantidades terrivelmente grandes (um tabuleiro de 27 x 27, por exemplo, oferece 234.000.000.000.000.000 soluções). Como o novo estudo aponta, quando a dimensão do tabuleiro atinge 1.000 x 1.000, com 1.000 rainhas, os computadores ficam travados, afundando em um abismo aparentemente interminável de cálculos.
Como o pesquisador princiapal Ian Gent, da Universidade de St. Andrews, aponta, soluções eficientes para o problema das oito rainhas permanecem indefinidas para programadores de computador, exigindo que os computadores se afundem nas possibilidades durante literalmente milhares de anos (o supercomputador fictício Deep Thought, de O Guia do Mochileiro das Galáxias, vem à mente, uma máquina que precisa de meio milhão de anos para calcular o significado de tudo). Gent tomou ciência do problema das oito rainhas depois de um amigo desafiá-lo a resolvê-lo no Facebook — um desafio que Gent e seus colegas agora transformaram em um estudo formal e em um prêmio de US$ 1 milhão oferecido pelo Instituto Clay de Matemática, com sede nos Estados Unidos.
Esse problema não é apenas um exercício hermético ou auto-indulgente para nerds de computador. Gent sente que um programa de computador que possa eficientemente resolver o problema das oito rainhas também seria capaz de resolver tarefas atualmente consideradas impossíveis, como descriptografar alguns dos mais difíceis protocolos de segurança na internet.
“Se você pudesse escrever um programa de computador capaz de resolver o problema muito rápido, você poderia adaptá-lo para resolver muitos dos problemas mais importantes que afetam a todos nós diariamente”, disse Gent em um comunicado de imprensa. “Isso inclui desafios triviais, como descobrir o maior grupo de seus amigos do Facebook que não conhece uns aos outros, até coisas mais importantes, como decifrar os códigos que mantêm todas as nossas transações online seguras.”
Como observado no artigo, os benefícios de tal programa seriam imensos, tanto em termos do que significaria para os campos da matemática, ciência da computação e inteligência artificial, mas também em termos de recompensas financeiras. A primeira equipe a quebrar este código, além de ganhar um milhão de dólares, seria a primeira a levar a tecnologia para o mercado.
Mas Gent e o coautor Peter Nightingale têm suas dúvidas sobre a possibilidade de que alguém vá resolver esse enigma em breve. O problema tem a ver com o número de opções que estão disponíveis para o computador, e a questão do backtracking, em que um algoritmo considera cada opção possível para um problema e depois abandona, ou “recua”, a partir de uma solução aparentemente inválida até que a solução correta possa ser encontrada. Esse processo, mesmo para os computadores mais rápidos, pode levar anos.
“No entanto, tudo isso é teórico. Na prática, ninguém nunca chegou perto de escrever um programa que possa resolver o problema rapidamente “, disse Nightingale. “Então, o que a nossa pesquisa tem mostrado é que, para todos os efeitos práticos, isso não pode ser feito.”
Se você procura uma explicação mais técnica para esse problema, formalmente conhecido como o problema P vs NP, sugiro que dê uma olhada no excelente artigo de Mike James no I Programmer. O artigo na Wikipédia (em inglês) sobre o problema das oito rainhas também é muito bom.
fique por dentro das novidades giz
Inscreva-se agora para receber em primeira mão todas as notícias sobre tecnologia, ciência e cultura, reviews e comparativos exclusivos de produtos, além de descontos imperdíveis em ofertas exclusivas
