É mais fácil para uma criança mandar um 1080 no skate?

Um skatista de 12 anos, Tom Schaar, recentemente se tornou a primeira pessoa da história a mandar um 1080 em um skate. É um feito impressionante, o que fez algumas pessoas questionarem se não foi mais fácil para Schaar devido ao fato de ele ser uma criança. Nossos amigos da Wired examinaram a questão.

O 1080 (uma abreviação de 1080º, só para ficar claro) foi feito por um skatista de 12 anos chamado Tom Schaar. Muito legal, mesmo. Mas e a questão principal? Seria mais fácil para uma criança fazer isso? É hora de um cálculo rápido.

Modelo 1080

O que é importante em um 1080? Bem, você precisa estar no ar para poder girar. Se eu assumir que ambos criança e adulto ficassem no ar a mesma quantidade de tempo, isso significa que a velocidade angular é importante. Não entremos nos números; digamos apenas que você precisaria rotacionar 1080º em um intervalo de tempo de ?t. Como o skatista começa com velocidade angular zero, ele precisaria de alguma aceleração angular durante a parte do lançamento.

Deixe-me começar com um modelo simples. Suponha que a criança e o adulto sejam dois cilindros. (Se eles fossem vacas, seria esféricos.) Aqui vai um diagrama.

Estou apenas assumindo que o adulto tem as mesmas proporções da criança, mas é maior. Uma vez e meia maior, no caso. Então, como você faz um cilindro ter aceleração angular? Você precisa de torque. Suponha que exista uma força empurrando esses cilindros durante o estágio de salto para aumentar a velocidade angular. Poderia escrever:

Aqui, você pode ver que estou fazendo aproximações. Neste caso, assumo que a força é perpendicular ao eixo e está na beirada do disco-humano. Eu não disse o que Fa e Fk são (para força do adulto e da criança, respectivamente). Chegarei nisso depois. Entretanto, na dinâmica de um corpo rígido rotacional eu posso dizer o seguinte:

Todos esses deveriam ser na verdade vetores, mas estou tentando manter o modelo simples. Aqui, o I é o momento de inércia sobre o eixo de rotação (ou como gosto de chamá-lo, a massa de rotação) e ? é a aceleração angular. Para um disco rodar em seu eixo central, I tem um valor:

Um I menor significa que será mais fácil alterar o movimento angular do objeto. Colocando isso e resolvendo para a aceleração angular, eu tenho:

Aqui você já pode adivinhar que o garoto talvez tenha alguma vantagem por ele ter um R menor. Claro, a criança não será capaz de empurrar com tanta força (F), o que significa que…? Que devemos continuar trabalhando. Vamos assumir que a criança e o adulto tenham a mesma densidade (?). Isso significa que eu poderia descrever a massa como:

Agora a minha expressão para a aceleração angular é:

Como isso afeta a criança e o adulto? Aqui vão as duas acelerações angulares usando os valores acima:

Para que o adulto tenha a mesma aceleração angular da criança, a força do adulto teria que ser cinco vezes maio que a da criança. Poderia ser? Acho que não. Por quê? Se você está andando em um skate, o que o faria começar a girar? De fato, a força viria da força de atrito lateral entre as rodas do skate e a pista. Se for este o caso, eu assumiria a expressão a seguir para a força de atrito máxima (mas não pra valer, já que eles estariam em uma superfície plana).

Como dito, isso está errado. A força norma não seria igual ao peso porque durante o salto, eles não estão em uma superfície plana. Entretanto, isso não importa. Por quê? Porque existirá o mesmo coeficiente na frente do termo mg. Esse coeficiente será o mesmo para a criança e para o adulto já que ele depende muito mais do ângulo. O ponto é que a força de atrito máxima será mais proporcional à massa. Deixe-me dizer que a força de atrito é apenas proporcional à massa e colocar isso na expressão. (usarei uma constante proporcional de K: )

O adulto ainda perde. A perda apenas não parece mais tão ruim. Mas espere. Isso é só uma estimativa. Eu não incluí coisas como o time de aceleração. Talvez o adulto teria um “tempo de salto” maior de modo que mesmo com uma aceleração angular menor, ele poderia alcançar a mesma velocidade angular. Ou talvez o adulto consiga pular mais alto. Ou talvez a criança pudesse usar um skate maior e aumentar o R apenas para a parte onde a força é aplicada e ter assim uma vantagem ainda maior.

No geral, eu classificaria isso como uma daquelas coisas onde o maior não quer dizer o mesmo. Eu caí nessa armadilha também. Parece que se você construir uma versão menor de um trem, ele poderia ser simplesmente como um grande trem. Infelizmente, as coisas nem sempre escalam da maneira como imaginamos.

Atrás de um papelzinho

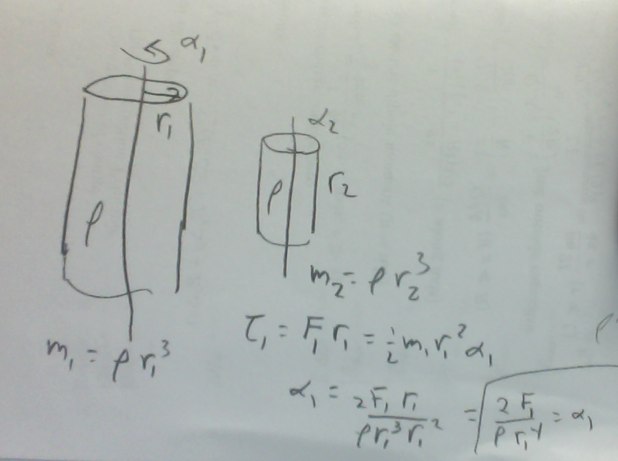
Quando essa pergunta pipocou no Twitter, eu fiz uma versão super rápida desse cálculo em uma folha de rascunho. Eis o que escrevi:

A mesma ideia, mas com algumas coisas deixadas de lado. Atenção: eu NÃO estou dizendo que para chegar ao 1440 você deveria começar a treinar seu irmão ou irmã de 6 anos. Se eles quiserem andar de skate, ok. Desde que o façam com segurança. Segurança sempre, crianças.

Wired.com tem expandido o consciente coletivo com tecnologia, ciência e notícias da cultura geek desde 1995.