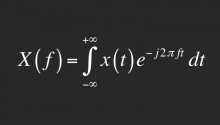Esta é a transformada de Fourier. Você tem que agradecer a ela pela música que ouve no streaming todos os dias, por espremer as imagens que você vê na internet em pequenos arquivos JPG, e até mesmo pela tecnologia dos fones de ouvido com cancelamento de ruído. Eis como ela funciona.
A equação permite aos matemáticos compreender rapidamente a frequência de qualquer tipo de sinal. É uma façanha. E não sou só eu que estou dizendo: em 1867, o físico Lord Kelvin também expressou seu amor eterno por esta obra da matemática. Ele escreveu: “o teorema de Fourier não é apenas um dos mais belos resultados da análise moderna, mas podemos dizer que ele fornece um instrumento indispensável no tratamento de quase todas as perguntas recônditas na física moderna”. E é assim até hoje.
A matemática da separação
A transformada de Fourier foi desenvolvida pelo matemático Jean-Baptiste Joseph Fourier e publicada em seu livro A Teoria Analítica do Calor, de 1822. Ele estava interessado em como o calor fluía para dentro e em torno de materiais. No processo de estudar este fenômeno, ele obteve sua transformada. Na época, ele não teria como perceber como era importante a contribuição que estava dando — não apenas à matemática e à física, mas também à engenharia, à tecnologia e à ciência como um todo.
Sua maior descoberta foi perceber que os sinais complicados poderiam ser representados através da simples soma de uma série de sinais mais simples. Ele escolheu fazer isso por meio da soma de senoides — aquelas ondas oscilantes que você viu na escola, que vagueiam entre o pico e o vale com regularidade previsível. Digamos que você toca três teclas em um piano. Você produz três notas diferentes, todas com frequências bem definidas — chamadas de altura, quando estamos falando de som — que parecem ondas senoidais. Assim:
Mas ao somá-las, aquele agradável acorde parece bem mais bagunçado. Assim:
Parece complicado, mas sabemos que, fundamentalmente, são apenas três ondas senoidais agrupadas no tempo e somadas. A grande sacada de Fourier foi perceber que, por mais complicada que seja a forma da onda final, ela sempre pode ser representada como uma combinação de senoides — mesmo que isso signifique usar um número infinito.
A genialidade dessa descoberta, para mim, é que, se você pode descobrir quais senoides precisam ser adicionadas para criar a forma da onda final, você sabe exatamente quais as frequências das ondas que precisam ser somadas — e em quais quantidades — para representar o sinal. Com esse conhecimento, você sabe o conteúdo exato da sua onda resultante.
Isso é o que a equação na parte superior da página faz em uma só tacada. O termo x(t) representa o grande e complicado sinal que você está tentando representar por mais simples. O termo e-jπ2ft parece um pouco assustador, mas na verdade é apenas o que os matemáticos usam para representar essas senoides de que estamos falando.
A parte legal é que multiplicá-los e colocá-los juntos numa integral — aquela linha curva na parte da frente e o dt no final — permite que a equação separe um por um os componentes das senoides que são necessários para representar o sinal. Assim, o resultado da equação, X(f), fornece a magnitude e tempo de atraso de cada um dos sinais simples que você precisa somar.
Isto é a transformada de Fourier: uma função que explica exatamente que frequências estão sobrepostas no sinal original. Isso pode parecer trivial, mas não é.
Transmitindo música…
Imagine que você trabalhe com o envio de arquivos de áudio pela internet. Você poderia simplesmente mandar a música inteira na forma como a gravadora a registrou, só que o arquivo é grande demais quando está desse jeito. A razão para o seu tamanho é que é uma gravação sem perdas, completa: cada frequência é preservada desde a gravação, por toda a mixagem, até a faixa final. Aplique a transformada de Fourier em um pequeno trecho de uma música, no entanto, e você vai descobrir que existem alguns componentes de frequência que são incrivelmente dominantes e outros que mal aparecem.
O formato de arquivo MP3 faz exatamente isso; ele também joga fora os componentes de frequência quase imperceptível para economizar espaço, bem como alguns dos que estão na extremidade superior de nossa faixa de audição, porque temos dificuldade de distinguir entre essas frequências.
Ele faz isso por toda a música, cortando-a em milhões de trechos, determinando os componentes de frequência importantes e jogando fora aqueles que são sem importância. O que resta são apenas as mais importantes frequências — ou notas — que podem ser tocadas em seus ouvidos para representar (com bastante precisão) a música original. Ah, e este arquivo tem menos de um décimo do tamanho original.
Também é muito semelhante à forma como funciona o Ogg Vorbis, o tipo de arquivo usado pelo Spotify em seu aplicativo de desktop. Na verdade, o Vorbis usa uma versão computacional extremamente rápida da transformada de Fourier, chamada de transformada discreta de cosseno, mas em termos gerais é a mesma ideia.
Aliás, o Shazam usa essas mesmas transformadas: ele tem um banco de dados de frequências distintas em canções, que ele compara com o que você coloca para o app ouvir, porque isso é mais confiável do que tentar comparar uma gravação de áudio com outra.
E, já que estamos falando de áudio, os fones de ouvido com cancelamento de ruído também usam transformadas de Fourier: um microfone grava o ruído do ambiente ao seu redor, mede o conteúdo da freqüência em todo o espectro, e, em seguida, inverte o conteúdo para adicionar um som em seu mix de áudio que vai anular os bebês chorando e ruídos da estrada ao seu redor.
… e imagens
Mas a equação de Fourier não é um craque de uma jogada só, não. Até agora eu só falei sobre ondas temporais como áudio — mas a transformada foi desenvolvida, em primeiro lugar, para ajudar Fourier a resolver problemas relacionados com o fluxo de calor através de materiais. Isso significa que ela também funciona em problemas que são espaciais.
Para Fourier, isso significava somar simples tipos de fluxos de calor em 2D para representar os mais complexos. Mas, da mesma forma, a transformada de Fourier pode ser usada para construir imagens digitais de forma mais eficiente do que a fazê-lo de pixel a pixel.
Arquivos de imagem sem perdas têm a cor de cada pixel definida separadamente. Quando você salva como JPG, a imagem é dividida em pedaços pequenos e a transformada de Fourier é aplicada a cada um dos blocos. Ela fornece uma descrição das frequências espaciais sobre como cor e brilho variam ao longo deste pequeno pedaço da imagem. Assim como no caso de MP3, o JPG joga fora alguns componentes de alta freqüência, que, no caso de uma imagem, fornecem os detalhes nítidos.
Para a maioria de nós, nossos olhos não podem detectar diferenças sutis de cor. Portanto, jogar fora os componentes que dão a variação de pixel para a pixel não altera a aparência da imagem. Obviamente, se você aumenta a compressão, começa a jogar no lixo frequências mais baixas, também — e é aí que as coisas podem começar a ficar meio pixeladas, à medida que as variações de cor entre os sub-blocos se tornam mais aparentes.
Exceto para os ouvidos e olhos muito treinados, sistemas de compressão como MP3 e JPG são pouco perceptíveis na maioria das vezes — os sons e imagens ficam ótimos e ainda conseguem ocupar apenas uma fração do espaço que seus irmãos sem perdas demandam. Em outras palavras, eles transformam imagens e músicas digitais em coisas práticas, o que nos permite compartilhá-los facilmente — um feito absolutamente incrível para uma única equação. Sem dúvida Fourier, prático o suficiente para escrever um livro sobre o fluxo de calor, aprovaria.
Imagens por Christine Daniloff/MIT