
A soma 1 + 2 + 3 + 4 + 5 + … até o infinito é de alguma forma igual a -1/12
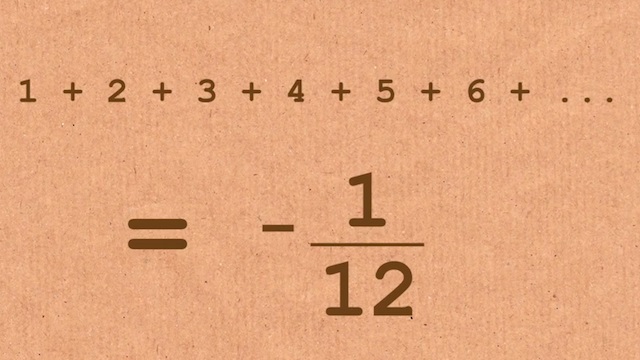
A soma de todos os números naturais, de um até infinito, não é um número ridiculamente grande como seria de esperar – é apenas -1/12. Sim, a soma de todos os números de um a infinito é uma fração negativa. Como assim?
Os físicos Tony Padilla e Ed Copeland, da Universidade de Nottingham, explicam ao Numberphile como se chega a este resultado. Você pode ver a alegria deles ao comprovar o resultado dessa somatória. Eu amo isso, e passei a gostar um pouco mais de matemática.
O vídeo possui legenda em português: clique na engrenagem para ativá-la.
Para compreender isto, você precisa entender que, de alguma forma, a soma 1 – 1 + 1 – 1 + … é igual a 0,5. Em seguida, com alguns truques matemáticos usando a sequência 1 – 2 + 3 – 4 …, você chega à somatória que resulta em -1/12.
Há muitas formas de mostrar que este resultado está correto: em outro vídeo, Ed Copeland explica outra prova mais formal. Na verdade, a ideia de que a soma de todos os números naturais é -1/12 surgiu em 1735, com o matemático suíço Leonard Euler. A prova formal veio mais de um século depois, graças à função zeta de Bernhard Riemann.
Esse tipo de somatória aparece o tempo todo na física, como no cálculo da energia de um elétron, que sabemos ser finita. Na teoria quântica, às vezes os físicos obtêm um termo infinito que eles simplesmente jogam fora – e funciona. Eles obtêm resultados teóricos, testam isso através de experimentos, e tudo se confirma.
Edward Frenkel, professor de matemática na Universidade da Califórnia em Berkeley, diz em outro vídeo do Numberphile:
Talvez este seja o segredo mais bem-guardado na física quântica: a maioria dos cálculos que os físicos fazem hoje em dia é assim. A resposta que eles obtêm parece infinita no começo, mas eles encontram formas de atribuir valores significativos para esse “infinito”, por assim dizer.
Claro, isso não é fácil de entender: a confusão acontece porque você está somando uma série infinita divergente, isto é, que não tende a um valor específico. O norueguês Niels Henrik Abel, que viveu no séc. XIX e deixou um enorme legado na matemática, uma vez escreveu: “as séries divergentes são a invenção do diabo, e é uma vergonha basear nelas qualquer demonstração que seja”.
Se você soma 1 + 2 + 3 + 4 + 5 + … até um bilhão, por exemplo, você terá um número enorme. Quanto mais você somar, maior ele fica. No entanto, como se trata de uma série infinita, você nunca pode parar de somar.
Lidar com essa somatória é algo contraintuitivo, mas é preciso seguir o conselho de Tony Padilla no vídeo: “você tem que ir até o infinito”.









