Como a Lei da Gravidade de Newton ajudou a nos levar para o espaço

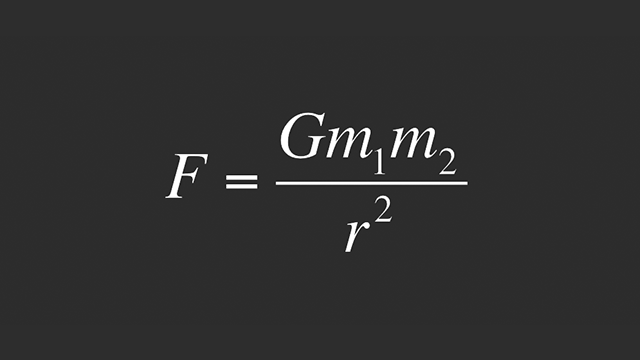
Tudo o que sobe tem que descer — mas nem sempre da forma que esperamos. Essa é a Lei da Gravidade de Newton, e você pode agradecer a ela pelo GPS, Google Earth e até pelas fotos registradas do outro lado do Sistema Solar. Eis os motivos.

A equação descreve a atração gravitacional que dois objetos têm um pelo outro, de acordo com a massa deles e com a distância entre o centro de cada objeto. É essa equação que prevê com qual força um objeto se choca contra a Terra quando é solto. Mas ela não resultou apenas do trabalho de Isaac Newton, apesar de levar o nome dele.

O poder usado pelo Sol para controlar os planetas

Por séculos, cientistas refletiram sobre o movimento das luas e dos planetas no nosso Sistema Solar, e muitos deles — de forma bem compreensível — acreditavam que tudo girava em torno da Terra. Foi só depois de Johannes Kepler aprofundar seus estudos no movimento de Marte, no início do século XVII, que a ideia de os planetas girarem em volta do Sol começou a tomar forma.

O que Kepler fez foi gerar três equações que descreveram, com uma exatidão impressionante, o movimento elíptico de satélites em órbita — como a Lua ao redor da Terra, ou Marte ao redor do Sol. O que ele não soube explicar foi como o corpo central mantinha os outros em sua órbita.

Muitos cientistas tentaram preencher essas lacunas. Em 1645, o astrônomo francês Ismael Bouleau sugeriu que “a força que o Sol exerce sobre os outros planetas… fica mais fraca e atenuada a distâncias maiores”. E ele estava certo, mas este raciocínio era dúbio; ele simplesmente comparou a força da atração a raios de luz.

Mais tarde, em 1666, Robert Hooke levou a mesma ideia além, adicionando que “estes poderes de atração operam de forma muito mais poderosa conforme o corpo está mais próximo do próprio centro”. Ele estava no caminho certo — mas não conseguiu elaborar uma conclusão.

Na publicação Philosophiæ Naturalis Principia Mathematica de Hooke, datada em 1697, Newton apresentou ao mundo a Lei da Gravidade. Ele juntou tudo o que havia sido estudado sobre o tópico anteriormente, formalizando o próprio pensamento na equação que ilustra este artigo.

Ela nos permite calcular a intensidade da força gravitacional, F, entre dois objetos conforme o produto dessas massas é divido ao quadrado da distância entre eles, r, tudo multiplicado pela constante gravitacional, G. (Entretanto, este último número é medido de forma experimental. Desde 2010, é usado o valor 6,67384 × 10⁻¹¹ m³/(kg · s²); ele será atualizado em 2018).

Houve reclamações de que Newton usava o trabalho de outros cientistas – mais notavelmente o de Hooke – como se fosse próprio. Mas em uma carta datada em fevereiro de 1697, Newton escreveu que “Se consegui ver além, é porque eu estava sentado sobre os ombros de gigantes”. Enquanto alguns estudiosos acreditavam que ele se referia de forma jocosa à estatura física de Hooke — ele era um homem bem baixo — é talvez mais agradável acreditar que este foi um raro momento de modéstia acadêmica de Newton.

A maçã

Então como foi que Newton teve sucesso onde outros falharam? Conforme diz a história, ele estava sentado sob uma macieira, quando um de seus frutos caiu na terra — e, crucialmente, em uma trajetória reta. Não de lado, ou na diagonal, mas reta. Naquele momento ele estava em Lincolnshire, um condado do Reino Unido, mas o mesmo ocorria em Cambridge, em Londres — e em qualquer outro lugar do planeta.

O que Newton descobriu é que a força gravitacional descrita por outros cientistas puxava objetos para o centro da Terra. Essa era a única forma que uma maçã poderia cair no chão da mesma forma em qualquer lugar. E ele notou que quanto maior a massa da maçã, maior a força que a atrai para baixo — e, correspondentemente, quanto maior a massa da Terra, maior a força da atração.

A descoberta de que a força agia em direção ao centro dos objetos foi vital. Isso, combinado ao conhecimento de que a força gravitacional diminuía conforme a distância, permitiu a Newton multiplicar a massa de dois corpos e dividir a equação através da distância da separação ao quadrado.

E faz sentido: se você imaginar que o campo gravitacional em volta de um objeto é uma série de esferas concêntricas todas desenhadas no centro deste objeto, então o mesmo campo gravitacional age em uma superfície mais larga conforme você se distancia. Dado que a superfície aumenta com a distância ao quadrado, r, então a força gravitacional deve diminuir na mesma escala.

Mas Newton continuou a pensar sobra a maçã: e se a árvore fosse maior? Ou muito maior? Muito, muito, muito maior, colocando a maçã na mesma altura que a Lua? Espera, por que a lua não cai do céu como a maçã, que tem os galhos da árvore para segurá-la?

A Lua está sempre caindo

A resposta para essa pergunta é que, de fato, ela está caindo. Mas, diferente da maçã, ela se move lateralmente. Newton refletiu sobre este problema não pensando na Lua, mas em uma bola de canhão. Atire uma bola de canhão horizontalmente do topo de uma colina e ela seguirá um caminho curvado, movendo-se horizontalmente, mas também para baixo, graças a atração gravitacional da Terra. Atire-a muito mais rapidamente e ela fará uma curva maior, mas continuará a cair na terra. Atire na velocidade certa — uma velocidade ainda bem rápida — e a velocidade horizontal dela será tão rápida que toda vez que a bola cair em direção à Terra ela também se moverá para frente, longe o bastante para a superfície da Terra ter se curvado na mesma quantidade.

É exatamente isso o que acontece com a Lua. Quando aquele pedaço rochoso que orbita a Terra surgiu, ele acumulou energia o suficiente para andar em movimento lateral pelo espaço sem cair na Terra, mesmo que ele esteja caindo a todo momento. E sem outras forças agindo sobre a Lua — não existe resistência do ar no espaço — ela continua indo, e indo, e indo.

É isso ao que nos referimos por órbita hoje — e a Lei da Gravidade de Newton permite a cientistas entenderem quanta energia lateral é necessária para mover um satélite nesta rotação, em vez de ele cair de volta para a Terra.

Pode ser surpreendente, mas uma única equação dá aos nossos cientistas informação o suficiente para colocar satélites na órbita do nosso planeta. Todos os satélites na órbita da Terra — esteja ele tirando fotos, enviando sinais de GPS, ou sendo a moradia para astronautas — foram colocados lá graças a essa equação.

Mas analise o movimento de qualquer um destes satélites conforme eles orbitam a Terra, e o percurso não confere com a dinâmica prevista nas forças da equação de Newton. Mas não é porque a equação está errada, é porque cada corpo no universo exerce uma força gravitacional em todos os outros. Obviamente, quanto maior e mais próximos eles estão, maior é a força — Newton exerceu forças muito menores na maçã, por exemplo, do que a Terra — mas isso não significa que cada problema pode ser solucionado por dois corpos.

A Lei de Newton somada aos computadores

A boa notícia é que a Lei da Gravidade de Newton é na verdade chamada de Lei da Gravitação Universal de Newton. Isso significa que você pode calcular todas as forças exercidas por corpos diferentes, para descobrir qual deles são realmente importantes. A má notícia é que a matemática necessária para calcular o movimento resultante dos corpos baseadas nestas forças não é a matemática que pode ser solucionada na base do papel e caneta.

Inclusive, em 1890, quando o matemático francês Henri Poincaré tentou descrever o movimento resultante de três corpos — neste caso uma estrela, um planeta e a uma partícula de poeira — ele disse que ficou “tão preso à complexidade dessa figura que não vou nem tentar desenhá-la”. Poxa vida.

Felizmente, surgiram os computadores, permitindo que as forças previstas na equação de Newton fossem calculadas em detalhes minuciosos. Inclusive, os físicos usaram o crescente poder computacional para combinar as forças geradas pelos maiores corpos do nosso Sistema Solar, e mapear onde a gravidade apresenta efeitos maiores — e onde ela era anulada.

Ocorre que existe uma série de tubos interligados pelo espaço de atração gravitacional constante (e ou baixa); eles agora são chamados de Rede Interplanetária de Transporte. Pense neles como trajetos de uma montanha que são mais fáceis de seguir do que subir verticalmente. Dispare uma espaçonave nesta rede e ela pode navegar com pouca energia; isso torna fácil viajar pelo espaço sem gastar muito combustível.

Inclusive, estes tubos são agora usados para enviar satélites a grandes distâncias do nosso Sistema Solar. O Genesis da NASA e a sonda espacial Solar e Heliospheric fizeram uso dos tubos; a China enviou a sonda Chang’e 2 para o asteroide 4179 da mesma forma. E isso, junto ao crescimento do poder computacional, é tudo graças à Lei da Gravidade de Newton. Nada mal para uma maçã.

Imagens por Image Editor/Flickr; EPA; NOAA Photo Library/Flickr