Talvez você já tenha ouvido falar do famoso problema P versus NP. Se você puder provar ou desmentir sua equação enigmaticamente curta, você seria um milhão de dólares mais rico – e talvez até bilhões de dólares mais rico, dependendo dos seus princípios morais.
A importância de P versus NP é principalmente o tipo de consequência que essa equação pode trazer para a computação. Acontece que este é um dos sete Problemas do Prêmio Millennium, o que significa que o Clay Mathematics Institute de Cambridge, Massachusetts, concederá US$ 1 milhão para quem conseguir provar ou refutar o problema. Mas se você provar que P, na verdade, é igual a NP, você nem precisaria do prêmio de US$ 1 milhão. Como o cientista da computação teórico Scott Aaronson explicou na semana passada em uma palestra em um auditório lotado no Los Alamos National Lab, no Novo México, provar que P=NP abriria algumas possibilidades intrigantes.
“Se alguém provar que P=NP, a primeira coisa que eles devem fazer é roubar US$ 200 bilhões em bitcoin. A segunda coisa que eles devem fazer é resolver todos os outros problemas do Millennium Prize”, disse Aaronson.
Para entender isso, você precisa saber que os computadores são dispositivos que resolvem problemas, resumidos em códigos capazes de serem lidos pelo dispositivo de computação física, com base nos princípios apresentados por Alan Turing. Resolver problemas requer várias etapas e um determinado período de tempo, sendo que esse tempo necessário aumenta à medida que o problema aumenta.
“P” refere-se aos problemas que os computadores resolvem o tempo todo, desde algo tão simples quanto a multiplicação de dois números até tarefas mais complexas, como navegar na Internet. À medida que um problema cresce em complexidade, o tempo necessário para resolvê-lo aumenta em “tempo polinomial”, em que um polinômio é um número com uma potência e um coeficiente (como n2). Se um problema é solucionável em n2 vezes e você dobra o tamanho do input, então a quantidade de tempo que levaria para resolver aumentaria em quatro vezes.
Ainda assim, existem muitos problemas em que se pode determinar que uma resposta está correta em tempo polinomial, mas, na verdade, chegar a essa resposta pode ou não ser possível em tempo polinomial. Estes são chamados de “tempo polinomial não determinista” ou problemas NP. O Sudoku é um problema NP – difícil de resolver, fácil de verificar. Outro exemplo importante hoje é fatorar grandes números em números primos. Por enquanto, pelo menos, leva um tempo muito longo – mais lento que o tempo polinomial – para fatorar números muito grandes em números primos, mas verificar se uma resposta está correta é tão simples quanto multiplicar os números resultantes juntos. De fato, essa ideia exata é a base da criptografia moderna, que consiste em gerar chaves de segurança fáceis de verificar, mas difíceis de decifrar.
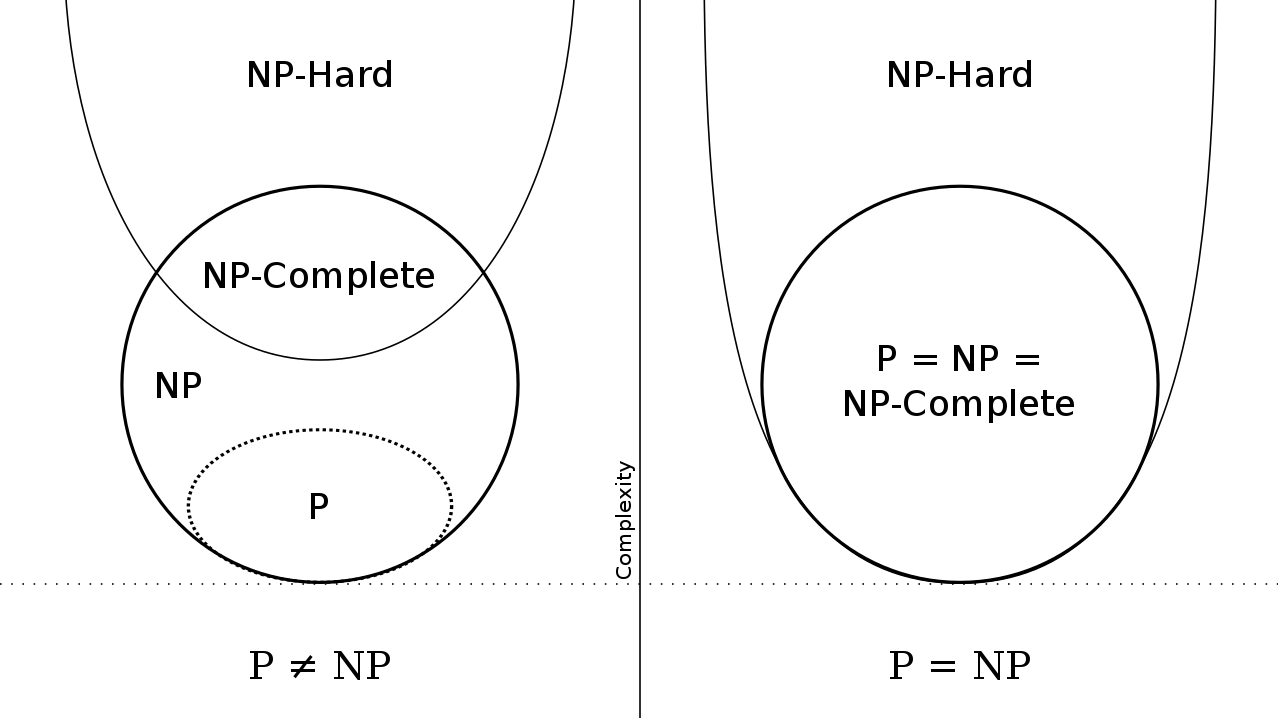
Novas provas matemáticas descobriram e podem continuar a descobrir soluções P para alguns desses problemas NP. O problema P versus NP pergunta se todo problema NP tem uma solução P, ou se existe algum problema NP que absolutamente não pode ser resolvido em P. Parece que deveria ser óbvio que P não é igual a NP, mas isso não é rigorosamente comprovado matematicamente. E se você provar que P é igual a NP, você também terá demonstrado que existem algoritmos de tempo polinomial para muitos problemas computacionais importantes. Você pode ficar muito rico – a mineração e chaves de segurança do bitcoin depende de problemas NP difíceis de resolver e fáceis de verificar.
Computadores quânticos, que são baseados em matemática diferente de computadores tradicionais, não prometem soluções P para todo problema NP. Antes pensava-se que eles poderiam ser capazes de resolver a classe mais difícil de problemas NP, chamados de problemas NP-completos. Se você pudesse encontrar uma solução eficiente para eles, você seria capaz de encontrar soluções eficientes para todos os problemas NP. Isso inclui o problema do vendedor ambulante e uma série de outros problemas de otimização semelhantes. Mas os computadores quânticos não satisfizeram esse entusiasmo. Em vez disso, eles são capazes de resolver alguns problemas P em um tempo mais curto (com um polinômio menor) ou mover alguns problemas NP para a generalização quântica de P, chamada BQP ou “Bounded-Error Quantum Polynomial Time” (ou, em tradução livre, “Tempo Polinomial Quântico Limitado ao Erro”).
Então vá em frente e tente provar que P é igual ou diferente de NP. Se você for bem-sucedido, você ganhará pelo menos um milhão de dólares, e talvez muito, muito mais. Se você não for bem-sucedido, bem, espero que você tenha levado uma vida com propósito pesquisando a teoria computacional.