Uma breve história do pi

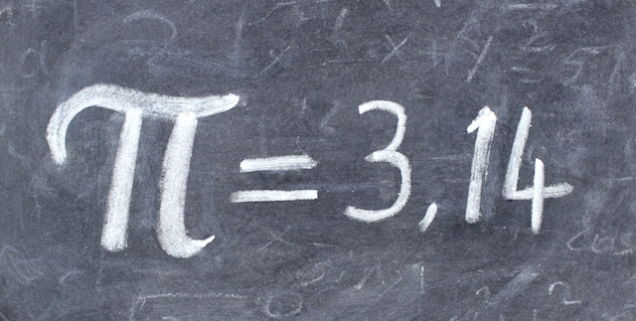
A razão entre a circunferência de um círculo e o seu diâmetro é uma constante. Isso é do conhecimento da humanidade desde tempos antigos; mesmo assim, apesar dos 2000 anos de reflexão, teorias, cálculos e provas, ainda hoje o valor exato do π permanece vago.

Civilizações antigas

Babilônios

Por volta do século XVII a.C. os babilônios tinham um conhecimento matemático avançado, gravado em tábuas complicadas que representavam quadrados, frações, raízes cúbicas e quadradas, pares recíprocos e até mesmo equações algébricas, lineares e quadráticas.

Não é surpresa, então, que esses gênios da matemática tenham discriminado também uma estimativa do π:

É uma estimativa muito boa, considerando que eles calculavam com os dedos – uma teoria para o desenvolvimento da matemática babilônica, que funcionava em um sistema numérico de base 60, é que eles usavam as 12 juntas dos dedos (sem contar o polegar) multiplicadas pelos cinco dedos da outra mão. Elegante.

Egípcios

Contemporâneos dos babilônios, os egípcios também fizeram grandes avanços na matemática. Acredita-se que foram os responsáveis por desenvolver o primeiro sistema numérico decimal completo.

A mais antiga evidência do π no Egito foi achada no papiro de Rhindi, datado por volta de 1650 a.C. Junto às instruções de multiplicação e divisão, evidência de números primos, frações e até mesmo algumas equações lineares, o π egípcio era computado como:

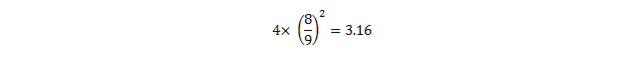
Hebreus

Enquanto os hebreus construíam o Templo de Salomão, por volta de 950 a.C., registravam suas especificações, incluindo a de uma grande fundição de bronze descrita em I Reis 7:23: “Fez o Mar de metal fundido, com dez côvados de diâmetro. Era redondo, tinha cinco côvados de altura; sua circunferência media-se com um fio de trinta côvados”.

Perceba que a razão entre a circunferência e o diâmetro é 3. Nada extremamente preciso, mas nada mal, considerando que eles haviam saído do deserto apenas alguns séculos antes.

Gregos

Os gregos avançaram bastante o estudo da matemática, particularmente no campo da geometria. Uma de suas missões mais antigas, datada pelo menos no século V a.C., era a “quadratura do círculo” — criar um quadrado com exatamente a mesma área de uma circunferência. Embora muitos tenham tentado, ninguém foi capaz de realizar o feito, e a razão disso permaneceu desconhecida por mais 2 mil anos.

Em todo caso, por volta do século III a.C. Arquimedes de Siracusa, o grande engenheiro e inventor, idealizou o primeiro cálculo teórico conhecido do π como:

Nessa época, o resultado de Arquimedes era por volta de 3,1418; de longe a melhor aproximação até aquela época.

Uns 400 anos depois, outro grego, Ptolomeu, refinou a estimativa do π usando as cordas de uma circunferência com um polígono de 360 lados, obtendo:

Chineses

Construída em uma base decimal de notação posicional por volta de 2000 a.C., a matemática chinesa já estava bastante desenvolvida no século III d.C., quando Liu Hui, que também desenvolveu uma forma primitiva do cálculo, criou um algoritmo para calcular π numa precisão de cinco casas decimais.

Duzentos anos depois, Zu Chongzhi calculou até a sexta casa decimal, demonstrando o seguinte:

Idade Média

Persas

Trabalhando durante o século IX d.C., Muhammad Al-Khwarizmi, amplamente creditado como criador de dois dos métodos mais fundamentais da álgebra (o balanceamento e a redução), pela adoção do sistema numérico hindu (de 1 a 9, com a adição do 0) e como inspiração para as palavras álgebra e algoritmo, acredita-se ter sido também o responsável por calcular o π precisamente até sua quarta casa decimal.

Algumas centenas de anos depois, já no século XV d.C., Jamshid al-Kashi apresentou o seu Tratado sobre a Circunferência, que calculava o π até sua décima-sexta casa decimal.

Era Moderna

Europeus

Dos tempos de al-Kashi até o século XVIII, avanços relacionados ao pi se limitavam apenas a produzir aproximações cada vez mais precisas. Por volta de 1600, Ludolph Van Ceulen calculou até sua 35ª casa decimal, enquanto em 1701, John Machin, creditado por criar métodos melhores para aproximar o π, conseguiu calculá-lo até seu centésimo dígito.

Em 1768, Johann Heinrich Lambert provou que o pi é um número irracional, o que significa que ele é um número real que não pode ser representado como o quociente de inteiros (lembre-se do cálculo de Arquimedes, onde o π existia entre dois quocientes de números inteiros, mas não era definido por um).

Houve novamente um intervalo nos estudos do π até que, no fim do século IX, mais duas coisas interessantes aconteceram: em 1873, William Shanks calculou corretamente 527 casas do pi (na verdade ele produziu 707 casas, mas as últimas 180 estavam incorretas). Em 1882, Carl Louis Ferdinand von Lindemann provou, em Über die Zahl, que o π é transcendente, o que significa que:

O pi transcende o poder da álgebra para que seja exibido em sua totalidade. Ele não pode ser expressado em nenhuma série finita de operações aritméticas ou algébricas. Usando uma fonte de tamanho fixo, ele não poderia ser escrito em um pedaço de papel tão grande quanto o universo.

Por ter provado a transcendência do pi, Lindemann também provou, de uma vez por todas, que não é possível calcular a quadratura da circunferência.

Americanos

No século XIX nem todo mundo estava atualizado nas novidades do mundo da matemática. Esse deve ter sido o caso do matemático amador de Indiana, Edwin J. Goodwin. Em 1896 ele estava tão convencido de que tinha, de fato, encontrado uma forma de achar a quadratura da círculo, que falou com um representante da Casa Estatal de Indiana, para apresentar um projeto de lei que formalizasse seu valor do pi como o correto.

Por sorte, antes que a legislatura de Indiana seguisse por um caminho sem volta, um professor da Universidade de Purdue que visitava o estado informou ao estimado corpo legislativo que era impossível encontrar a quadratura da circunferência e que, na verdade, a “prova” de Goodwin era baseada em dois erros. Deles, o mais pertinente para esse artigo é:

As mentes mais sensatas do senado prevaleceram e o projeto de lei foi deixado de lado, com a observação de um senador de que, de qualquer forma, seus poderes legislativos não se estendiam a definir verdades matemáticas.

Bônus:

O volume matemático de uma pizza é pizza. Como isso funciona, você pergunta? Bem, se z = raio da pizza e a = sua altura, então π * raio² * altura = pi * z * z * a = pizza.